Area and volume of a parallelepiped - Math Central
Parallelepiped - Wikipedia
Question Video: Finding the Volume of a Parallelepiped | Nagwa
Volume of Parallelepiped Formula - GeeksforGeeks
The Volume of a Parallelepiped
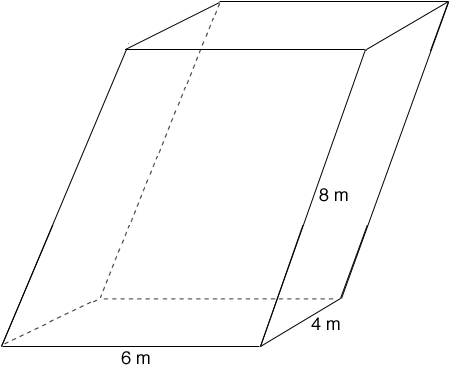
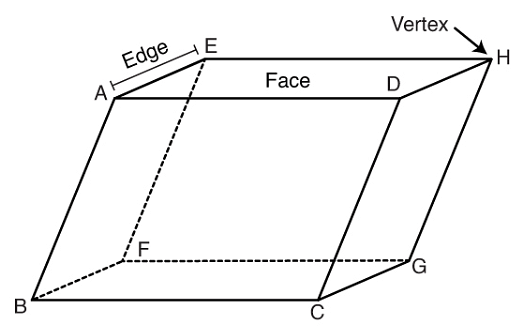
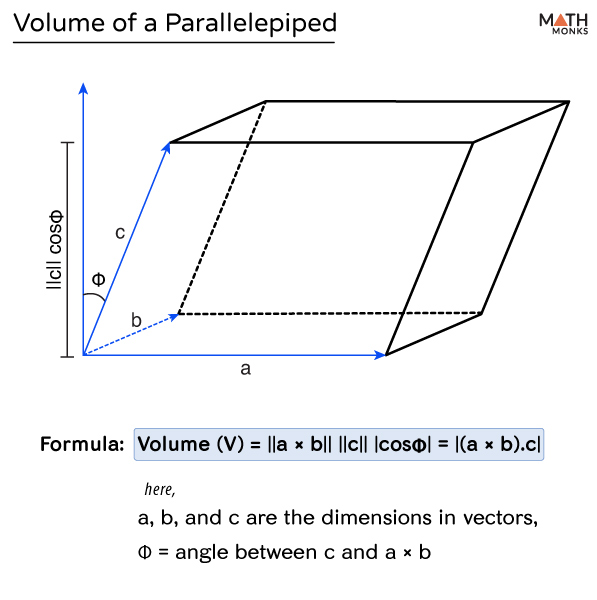
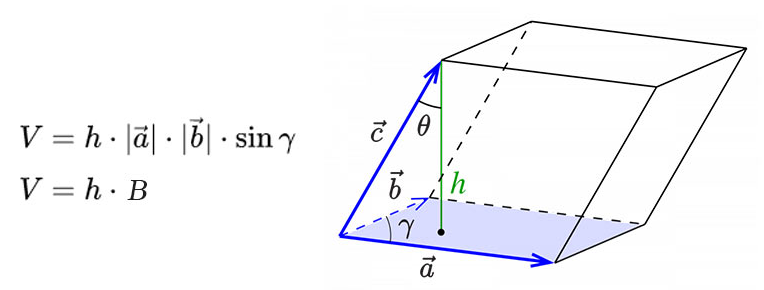
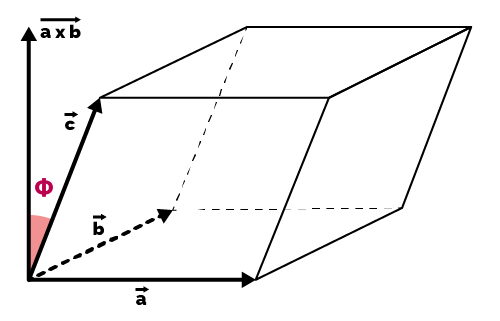
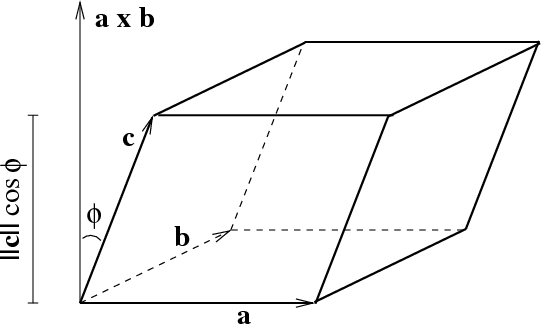
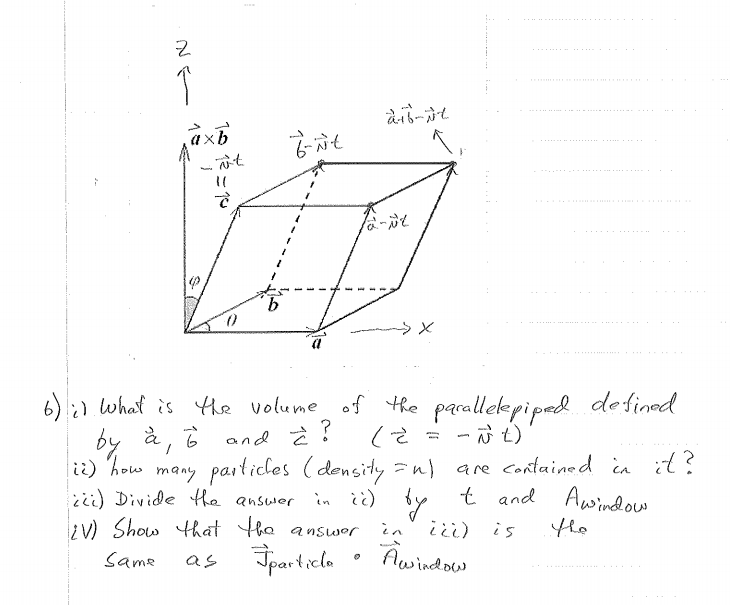
Find the volume of the parallelepiped whose coterminous edges are represented by the vectors.vec{a}=hat{i}-2hat{j}+3hat{k}, vec{b}=2hat{i}+hat{j}-hat{k}, vec{c}=hat{j}+hat{k}.
Volume of a parallelepiped using determinants (Applet 3.) | Download Scientific Diagram
Parallelepiped: Meaning, Properties & Formulas
Parallelepiped - Definition, Formulas, Examples, and Diagrams
Volume of Parallelepiped (Lesson With Examples & Solutions)
Volume of Parallelepiped Calculator
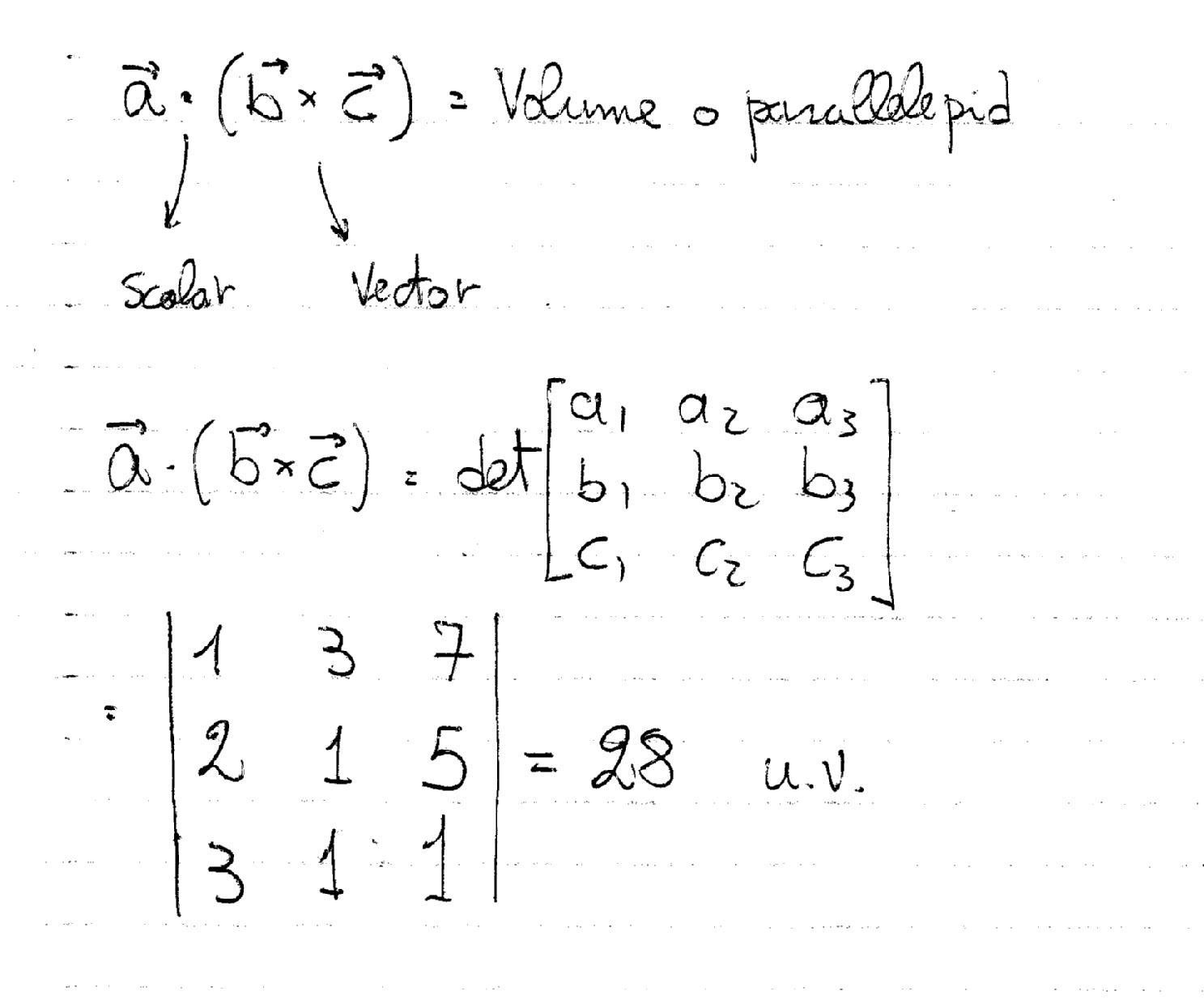
How do you find the volume of the parallelepiped determined by the vectors: <1,3,7>, <2,1,5> and <3,1,1>? | Socratic
File:Parallelepiped volume.svg - Wikipedia
Volume of a Parallelepiped Calculator
Question Video: Finding an Unknown Vector Component given the Volume of a Parallelepiped and Its Three Adjacent Sides in the Vector Form | Nagwa
Find the volume of the parallelepiped
Volume
Image: Volume of parallelepiped - Math Insight
Volume of the parallelepiped from vectors — Krista King Math | Online math help
Solved b) i) What is the volume of the parallelepiped | Chegg.com
multivariable calculus - volume of the parallepiped spanned by the vectors - Mathematics Stack Exchange
Find the volume of the parallelepiped whose coterminous edges are represented by the vectors.vec{a}=6hat{i}, vec{b}=2hat{j}, vec{c}=5hat{k}.
Parallelepiped - Formulas, Properties, Definition, Examples
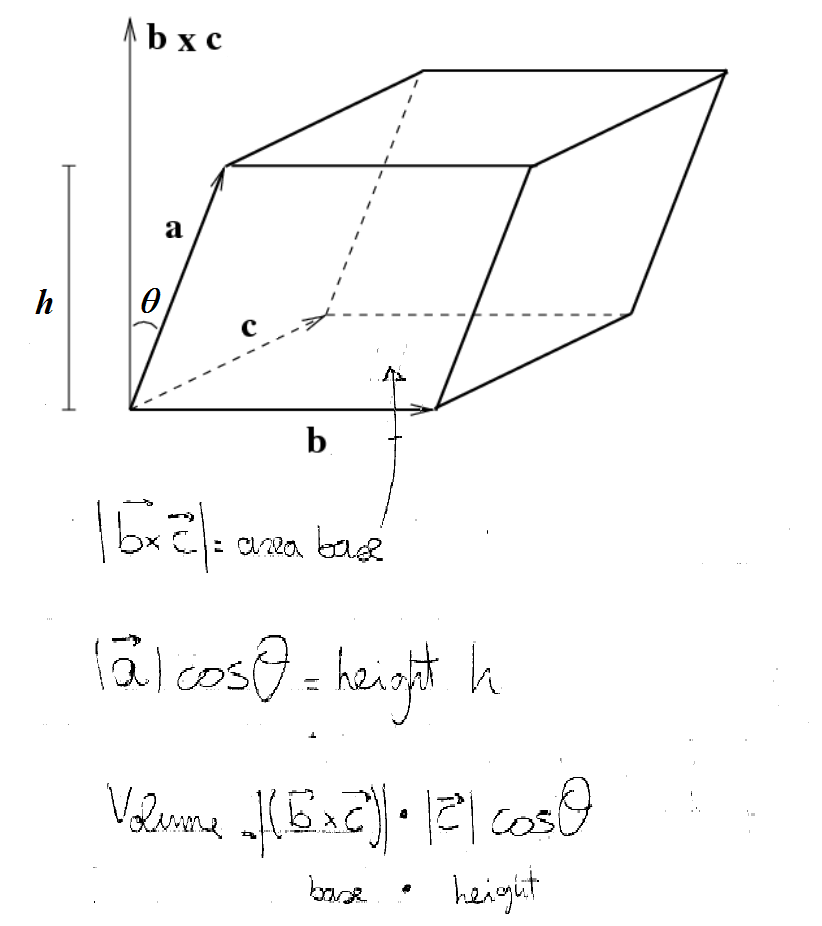
How do you find the volume of the parallelepiped determined by the vectors: <1,3,7>, <2,1,5> and <3,1,1>? | Socratic
Volume of a Parallelepiped Using The Triple Scalar Product Calculus 3 - YouTube
Volume of a Parallelepiped Calculator
Parallelepiped- Definition, Volume and Area Formula, Example
